矩阵乘法与Flash Attention优化笔记
一、分块矩阵乘法(Tiled Matrix Multiplication)
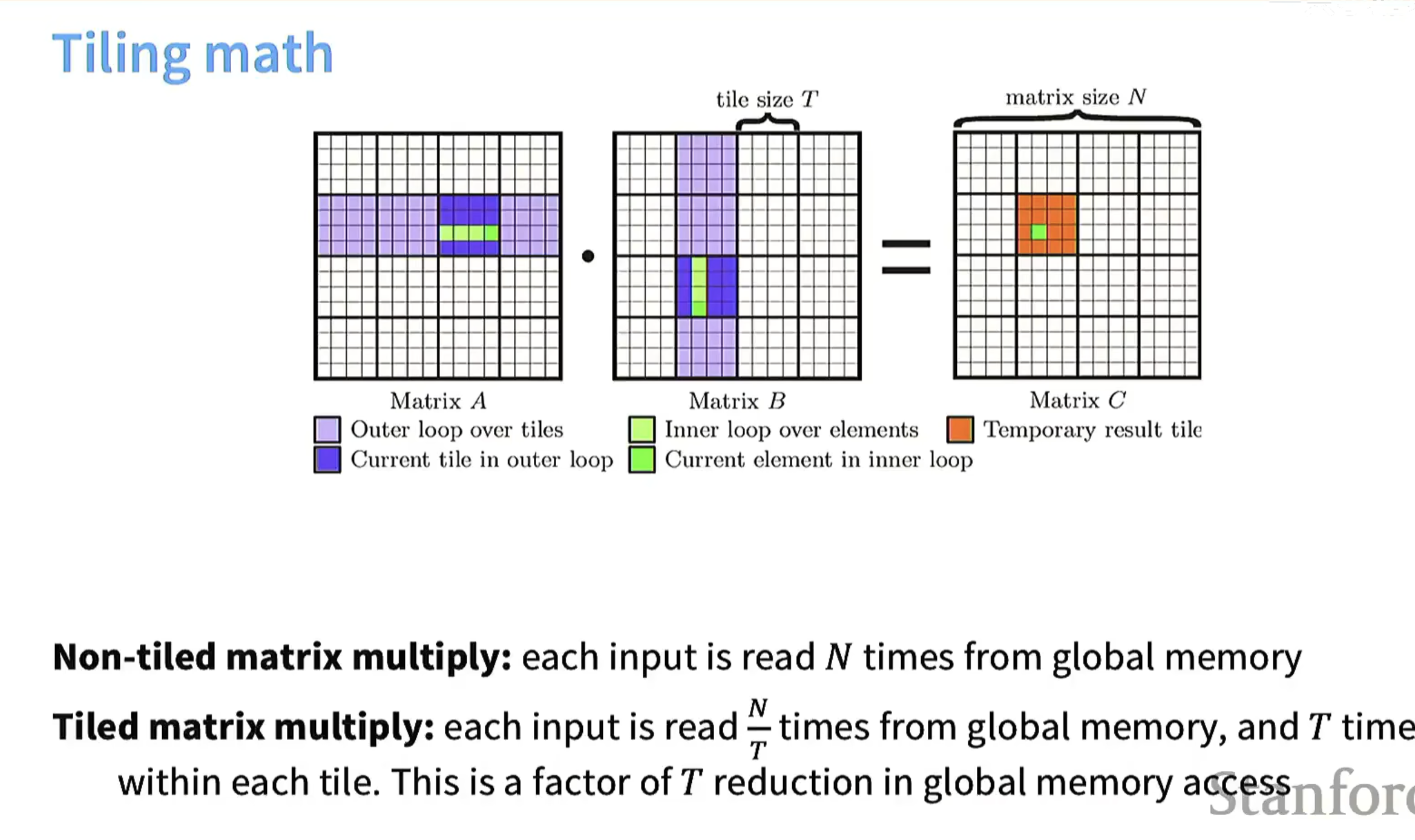
1. 核心原理
矩阵乘法基本式为
- 外层循环:遍历这些块(紫色部分为外层循环的块,深蓝色是当前外层循环处理的块)。
- 内层循环:在每个块内部,遍历块里的元素(绿色部分为内层循环的元素,亮绿色是当前内层循环处理的元素)。
- 结果计算:通过分块计算逐步得到结果矩阵C的临时块(橙色部分),最终整合为完整的C。
2. 内存访问优化
| 计算方式 | 内存读取次数 | 优势 |
|---|---|---|
| 非分块矩阵乘法 | 每个输入元素从全局内存读N次(N是矩阵规模) | 无 |
| 分块矩阵乘法 | 每个输入元素从全局内存读 |
内存访问次数减少为原来的 |
二、burst section相关
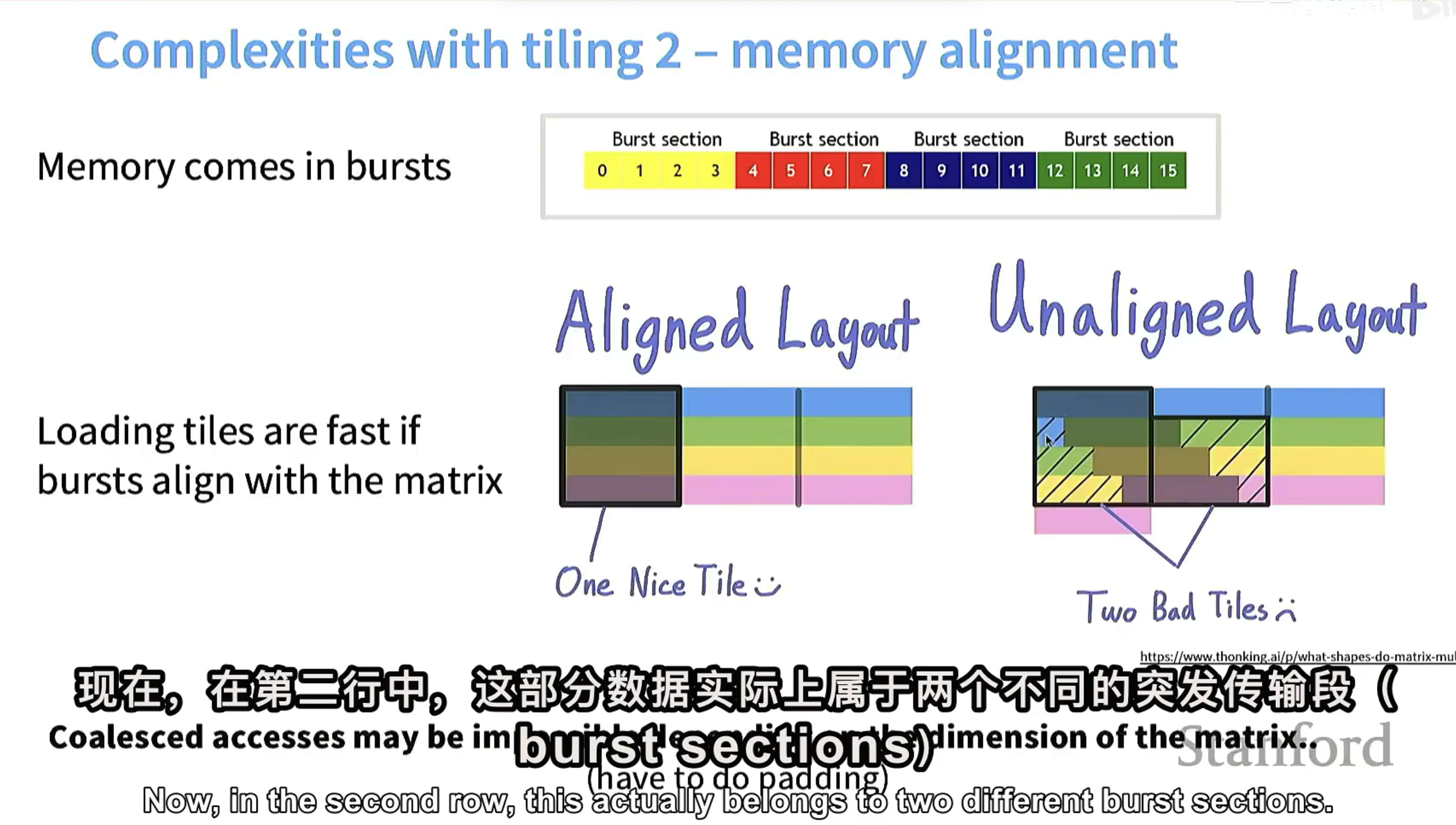
1. 所属硬件
“burst section”通常指GPU(图形处理器)中的概念,代表内存突发传输中的一个数据段。GPU为提高内存访问效率,采用成块(burst)读取数据的方式,而非逐个字节读取。虽CPU在缓存读取等操作中也有成批读取数据的概念,但在矩阵分块优化及相关术语使用语境中,尤其涉及大规模并行计算和内存访问优化时,更多在GPU计算加速场景下讨论。
2. 内存对齐与数据加载
- 内存对齐(Aligned Layout):当矩阵分块(tile)和内存突发传输段对齐时,GPU可高效加载数据,能一次性读取整个分块的数据,减少读取次数,提升性能(如“Aligned Layout”示例展示,快速加载“One Nice Tile”)。
- 内存未对齐(Unaligned Layout):若矩阵分块和内存突发传输段不对齐,一个分块的数据可能分散在多个突发传输段中,GPU需多次读取不同突发传输段获取完整分块数据,导致性能下降(如“Unaligned Layout”示例,产生“Two Bad Tiles”,数据加载效率低)。
三、方阵矩阵乘法性能图表(Matrix mystery)
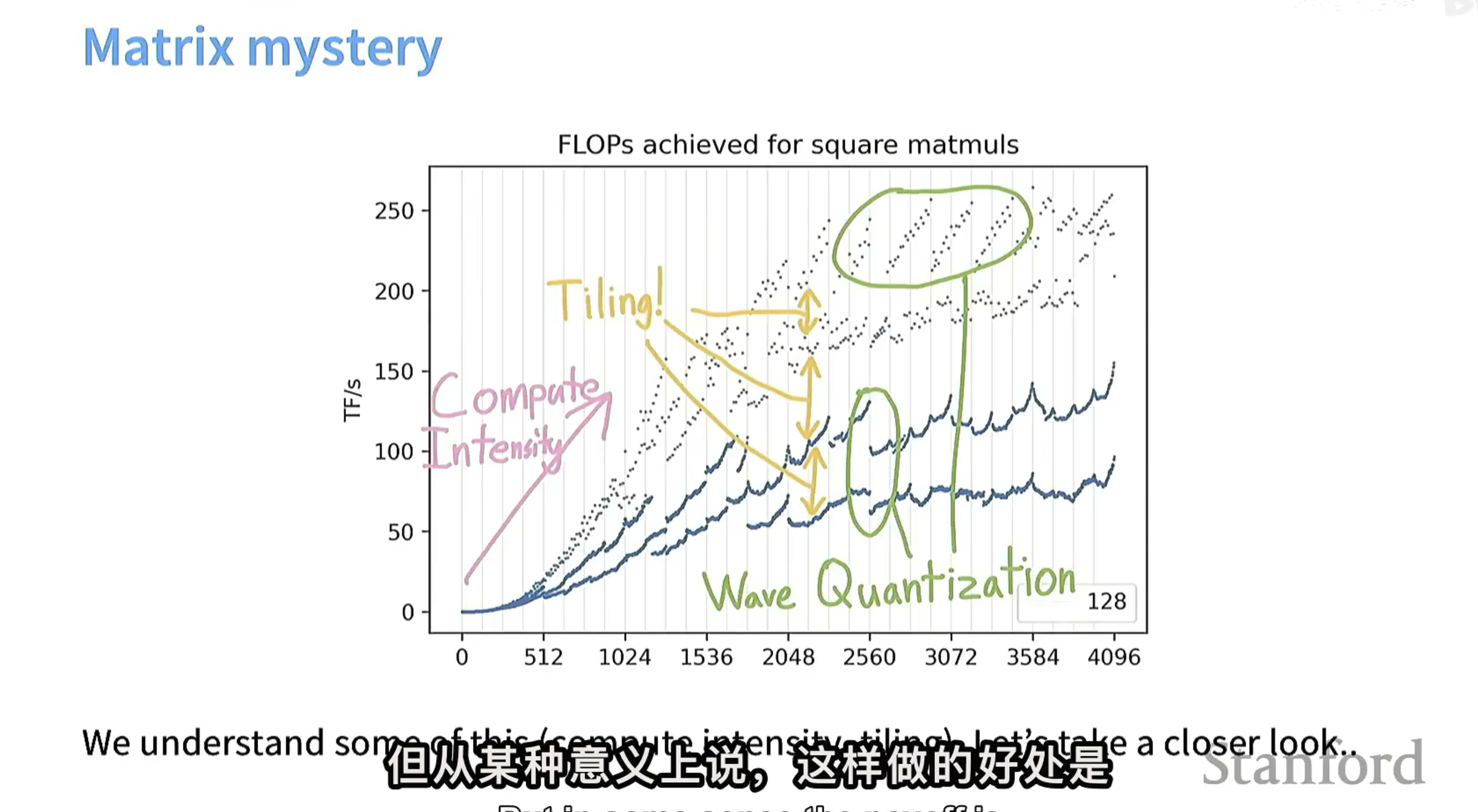
1. 坐标轴与核心指标
- 横轴:矩阵相关规模参数(如矩阵维度等)。
- 纵轴:TF/s(每秒万亿次浮点运算),衡量矩阵乘法计算性能。
2. 关键技术与趋势
- Compute Intensity(计算强度,粉色标注):随矩阵规模等因素变化,计算强度提升推动性能(FLOPs)上升。计算强度为“计算操作与内存访问的比例”,比例越高,计算越“密集”,能更充分利用硬件计算能力。
- Tiling(分块,黄色标注):经典优化手段,通过把大矩阵拆成小“块(Tile)”计算,减少内存访问开销、提升数据复用率,显著提高性能(黄色箭头指向区域性能因分块优化明显提升)。
- Wave Quantization(波量化,绿色标注):优化思路(可能涉及数据量化、压缩等,减少计算或内存传输开销),绿色圈出区域性能在该优化下有特定变化趋势。
3. 整体意图
标题“Matrix mystery”(矩阵之谜)及文字“We understand some of this (compute intensity, tiling)… let’s take a closer look…”体现:虽已理解“计算强度”“分块”等部分优化作用,但仍需深入分析这些技术(及“波量化”这类技术)如何共同影响矩阵乘法性能,探索其中“奥秘”。
四、不同k值与内存对齐关系
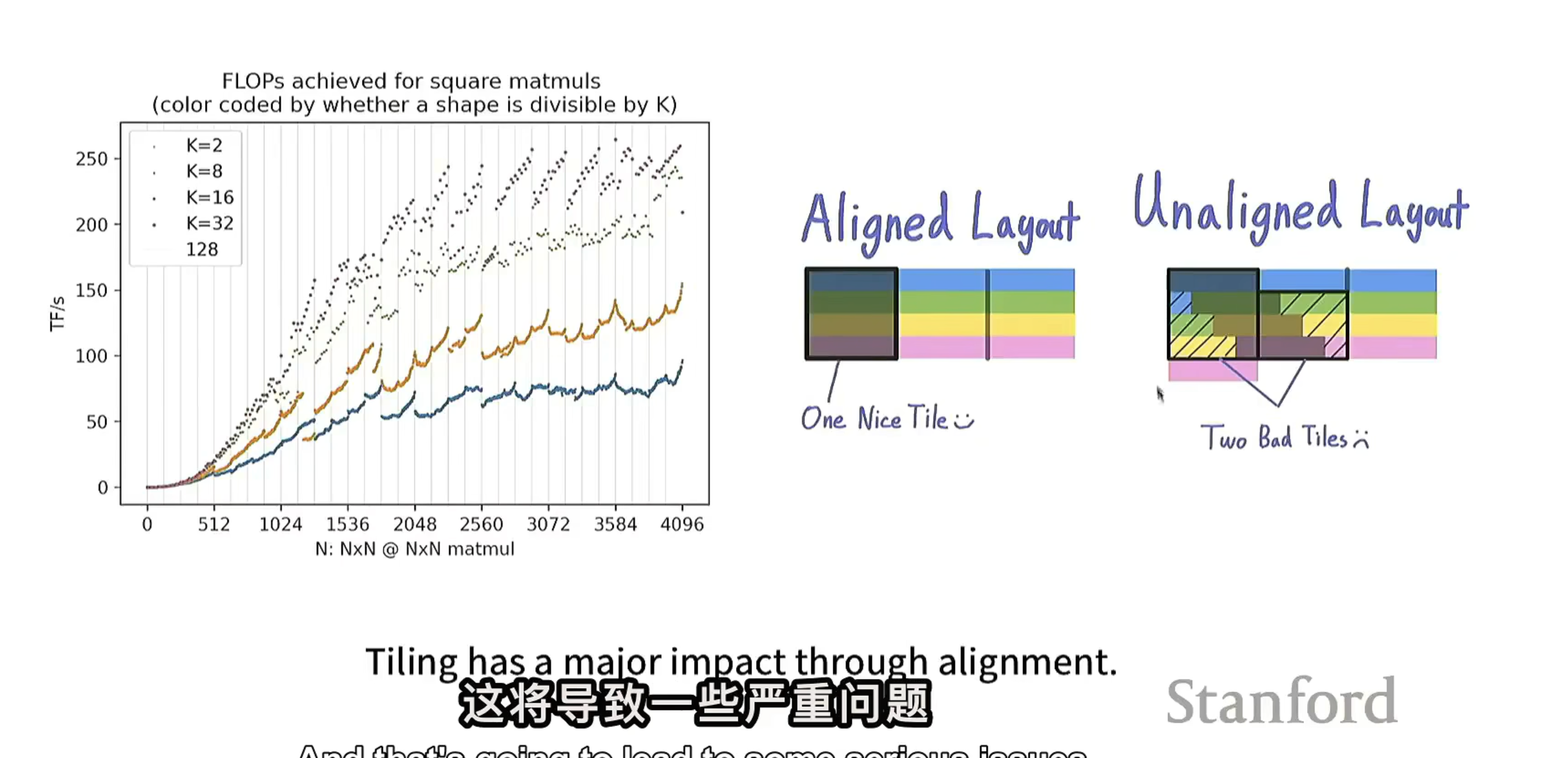
1. 基础关系
矩阵乘法分块优化(Tiling)中,内存对齐是关键因素。矩阵分块与内存突发传输段(burst section)对齐时,数据加载效率高;不对齐时,数据加载效率低。
2. 不同k值影响
K通常代表矩阵分块的某个维度参数(如分块大小或划分粒度),不同K值改变矩阵分块尺寸和形状,影响其与内存突发传输段匹配关系:
- 合适的K值(利于对齐):K取值使分块边界与内存突发传输段边界匹配(如分块尺寸是内存突发传输段大小的整数倍),加载分块数据时实现内存对齐,一次突发传输完整加载一个分块,数据加载高效。
- 不合适的K值(导致未对齐):K取值不合适,分块边界与内存突发传输段边界不匹配,一个矩阵分块数据可能跨越多个内存突发传输段,加载一个分块需多次突发传输,内存未对齐,严重降低数据加载效率。
3. 图表体现
不同K值(K = 2、K = 8、K = 16、K = 32)对应FLOPs曲线走势不同。不合适的K值因导致内存未对齐,数据加载效率低,影响整体矩阵乘法计算性能,FLOPs表现不如内存对齐情况。
五、Softmax计算(普通与在线)

1. 普通Softmax(Normal softmax,左侧)
- 公式:
,通过减去输入向量x中的最大值 进行数值稳定(避免指数运算数值过大溢出),计算每个元素的Softmax结果 。 - 算法(Algorithm 2: Safe softmax):
- 初始化最大值
为负无穷。 - 遍历输入向量x的每个元素
,逐步计算当前最大值 (找到整个向量的最大值 )。 - 初始化总和
为0。 - 遍历输入向量x的每个元素
,计算 并累加到 (得到分母的总和)。 - 对每个元素
,计算 ,得到Softmax结果。
- 初始化最大值
2. 在线Softmax(Online softmax,右侧)
- 算法(Algorithm 3: Safe softmax with online normalizer calculation):
- 初始化最大值
为负无穷,总和 为0。 - 遍历输入向量x的每个元素
: - 逐步更新当前最大值
。 - 在线更新总和
,利用前一次的最大值 和当前最大值m_j调整累加项( ),避免后续重复计算。
- 逐步更新当前最大值
- 对每个元素
,计算 ,得到Softmax结果。
- 初始化最大值
3. 核心差异
普通Softmax“先找全局最大值,再统一计算分母总和”;在线Softmax“边遍历元素、边更新最大值,同时在线维护分母总和”,在处理大规模数据或对计算效率(尤其是内存访问模式)有要求的场景下,在线Softmax可能更具优势(如更友好的缓存利用、流式计算特性)。
六、Flash Attention优化(含Softmax与输出部分)
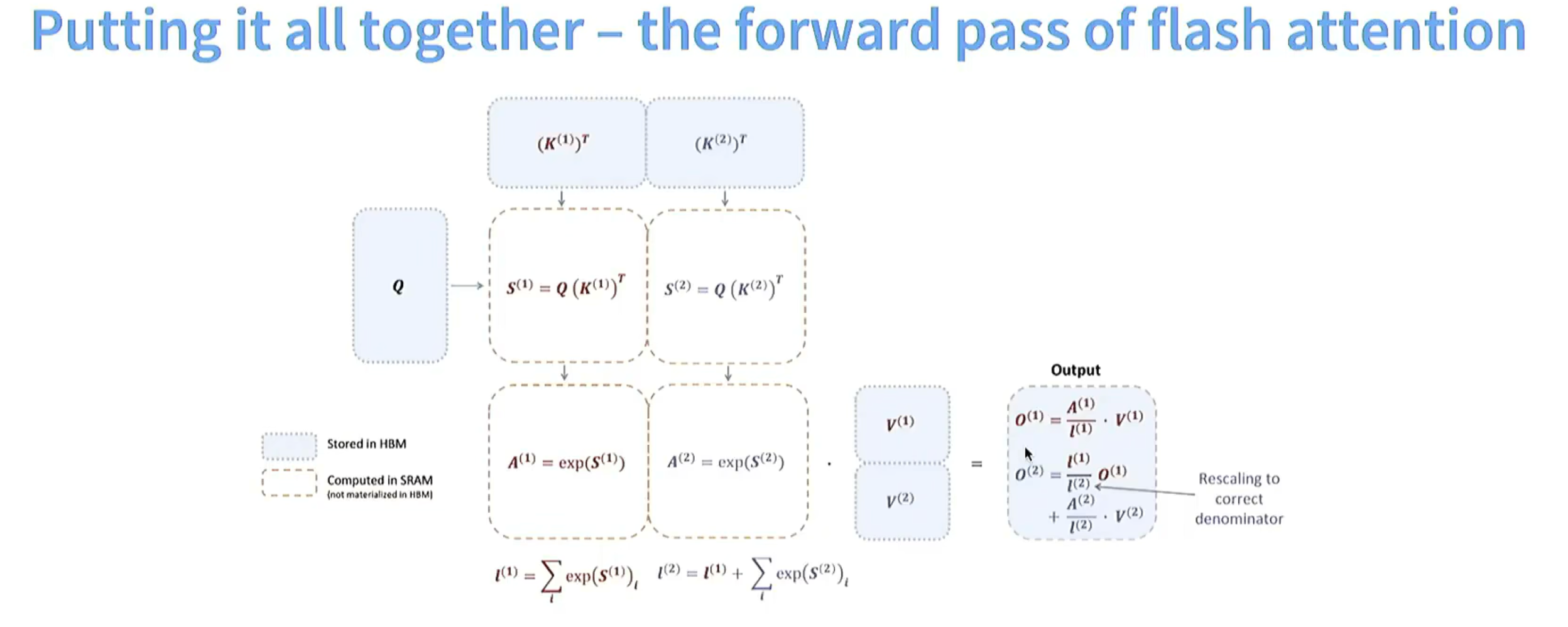
1. 整体优化方式
| 优化方式 | 具体操作 | 优势 |
|---|---|---|
| 分块计算(Tiling) | 键矩阵K分成多个部分(如 |
避免一次性处理大规模矩阵乘法,降低内存需求;更好利用GPU并行计算能力,提升计算效率 |
| 中间结果存储与复用优化 | 指数计算 |
复用之前计算结果,减少重复计算,节省计算资源和时间 |
| 避免完整softmax计算 | 不直接计算标准softmax,通过计算局部的归一化因子(如 |
减少计算量,序列长度较长时效果更显著 |
| 内存管理优化 | 标注不同计算步骤存储位置(如存储在高带宽内存(HBM)和在静态随机存取存储器(SRAM)中计算,且不在HBM中实例化) | 合理分配内存,减少数据在不同存储层级间传输开销;SRAM读写速度比HBM快,在SRAM中进行部分计算加快计算速度 |
2. Softmax节省计算细节
Flash Attention节省计算非对应“O(2)”这类计算,主要通过:
- 避免全局softmax的归一化计算:传统Attention计算softmax需对整个注意力得分矩阵归一化(计算所有元素指数值,再求和得到归一化因子,计算复杂度高,序列长度n较大时计算量随
增长);Flash Attention通过分块计算和增量式归一化因子计算(如计算 和 并复用 结果),避免全局softmax归一化计算,减少指数运算和求和运算次数。 - 分块矩阵乘法减少内存和计算开销:传统Attention计算注意力得分
对完整矩阵相乘(规模大时内存占用大、计算成本高);Flash Attention将键矩阵分块,查询矩阵分别与分块转置矩阵相乘,降低每次计算内存需求,适配GPU并行计算特性。 - 中间结果复用减少重复计算:传统Attention可能未充分复用中间结果导致重复计算;Flash Attention复用中间计算结果(如
依赖 ),避免重复计算指数和累加值。 - 内存层级优化减少数据传输开销:传统Attention数据在不同内存层级间频繁传输,传输开销大;Flash Attention合理安排计算和存储位置(如在SRAM中计算部分结果),减少数据传输,间接节省计算时间。
3. 输出部分(
核心逻辑
输出O是注意力权重与值(Value)矩阵的加权和,Flash Attention中输出拆分为
节省计算关键
- 复用
的结果:计算 时直接复用之前计算的 ,不重新计算与 相关的加权和,避免对 和 的重复运算,减少矩阵乘法和加权求和计算量。 - 增量式归一化(Rescaling):通过
的“重新缩放(Rescaling)”操作,将分块计算结果增量式合并,不对整个矩阵重新做全局softmax归一化,避免大规模矩阵重复归一化计算,节省指数运算和求和开销。
迭代方式优势
Flash Attention输出合并阶段采用增量式、复用中间结果的方式,处理后续tile(如
4. 实际分块方式
分块依据
- 内存层级适配:GPU有不同内存层级(SRAM速度快但容量小,HBM容量大但速度相对慢),分块大小设计成能让分块数据“刚好适配高速缓存(如SRAM)”,计算单个分块时数据留在高速缓存,减少慢速全局内存访问。
- 并行计算效率:分块能让GPU的线程束(Warp)或线程块(Block)高效并行计算,分块维度匹配GPU线程并行度,使每个线程或线程束“负载均衡”处理分块内计算。
实际分块动态性
分块大小非固定“两块”“三块”,而是动态调整:根据输入序列长度、模型隐藏层维度等参数,计算最优分块尺寸(如每个分块的token数量、特征维度等);例如长序列(几千甚至上万个token)会分成多个小分块,逐个处理,每个分块大小优化为“能让该分块的注意力计算在GPU上达到最高吞吐量”。
核心目的
让每个分块的中间结果(如注意力得分、softmax中间值)保存在高速内存中,避免频繁从低速全局内存读取/写入;让分块内的矩阵乘法、softmax等操作能被GPU高效并行执行,最大化FLOPS(每秒浮点运算次数)。
